数列 【数列まとめ】おさえておきた差がつく入試頻出・重要問題
等差、等比中項、シグマ公式の証明、和と一般項、部分分数分解、等差と等比数列の積の和、規則性、格子点、数学的帰納法(3タイプ：通常、2段仮定、全段仮定)、有名漸化式解放パターン、確率漸化式。厳選・頻出・重要入試問題まとめ。過去問演習。数列対策。東大、京大、旧帝大、GMARCH、関関同立対策。数学B：数列まとめ
数列 
漸化式 【2017大阪大学】対数型の漸化式(パターン16)｜数学B：数列
漸化式の解き方・解法まとめ。対数をとることで隣接二項間特性方程式型に帰着させる一般項の求め方。また数列の増減(増加数列)を調べることで考える問題。有名頻出・重要問題。定期考査、大学入試共通テスト、２次試験対策。2017阪大対策・過去問演習。
数列 【1994東京大学】π/5(36°)の三角比の値、2段仮定の数学的帰納法｜三角関数と数列
頻出π/5(36°)の三角比の値を加法定理、２倍角、３倍角を利用して求める。また差がつく入試問題の対称式と2段仮定の数学的帰納法について。1994東京大学過去問演習(類題：2017東大)。数学Ⅱ三角関数、数学B数列
数列 【大阪大学】対数関数で囲まれた領域内の格子点｜1
x,y座標がともに整数となる格子点の個数の数え方・考え方を解説。x＝kやy＝k上の格子点を数え、総和(シグマ)を考える。難関大学頻出・有名問題。差がつく入試問題。数学A：整数問題、数学B：数列。阪大過去問演習。GMARCH、関関同立、早慶、東大、京大、一橋、旧帝大、難関大学対策。
x,y座標がともに整数となる格子点の個数の数え方・考え方を解説。x＝kやy＝k上の格子点を数え、総和(シグマ)を考える。難関大学頻出・有名問題。差がつく入試問題。数学A：整数問題、数学B：数列。阪大過去問演習。GMARCH、関関同立、早慶、東大、京大、一橋、旧帝大、難関大学対策。
数列 【格子点】放物線と直線で囲まれた領域の格子点の個数｜お茶の水女子大学
x,y座標がともに整数となる格子点の個数の数え方・考え方を解説。x＝kやy＝k上の格子点を数え、総和(シグマ)を考える。難関大学頻出・有名問題。差がつく入試問題。数学A：整数問題、数学B：数列。お茶の水女子大学過去問演習。GMARCH、関関同立、早慶、東大、京大、一橋、旧帝大、難関大学対策。
数列 【格子点】x+y≦n(x,yは0以上の整数)を満たす格子点の個数｜2014中央大学
x,y座標がともに整数となる格子点の個数の数え方・考え方を解説。x＝kやy＝k上の格子点を数え、総和(シグマ)を考える。難関大学頻出・有名問題。差がつく入試問題。数学A：整数問題、数学B：数列。2014中央大学過去問演習。GMARCH、関関同立、早慶、東大、京大、一橋、旧帝大、難関大学対策。
数列 【2021九州大学】等差×等比数列の総和、実験→予想・推測→数学的帰納法(全段仮定)
等差数列と等比数列の積の和。与えられた漸化式から具体的に値を代入し一般項を予想。数学的帰納法を用いて証明。2021九大過去問対策・演習。数学B：数列の和と漸化式。全段仮定の差がつく入試問題。類題演習
数列 【2010京都大学】数学的帰納法(全段仮定)｜差がつく良問(数学B数列)
n≦kを満たすすべてのnで成り立つと仮定し，n=k+1のときに示す．数学的帰納法の有名３タイプのうちの「全段仮定法」．経験で差がつく入試問題．2010京大過去問演習・対策。数学B。また別解として背理法の紹介。
数列 【2003京都大学】23/111の小数第k位の数をak .Σak/3^kを求めよ．
循環小数から数列の規則性に注目し、nが3で割った余りで場合分け。式をまとめ、等比数列の和(シグマ)として考える。2003京大過去問演習。数学B：数列
数列 【2021金沢工業大学】分母が３つの積の部分分数分解
分子が等差数列，分母が連続する3つの整数の積である有理数からなる数列の和。恒等式を用いて2つの分数分解を行う。重要・頻出入試問題。数学B数列
数列 2乗の和の公式の証明｜Σk^2=1/6n(n+1)(2n+1)
1^2+2^2+3^2+・・・+n^2(2乗の和：6分の1の公式)について、(k+1)^3-k^3の形を利用した部分分数分解のように考える解法と、数学的帰納法を用いた２通り証明。Σ(シグマ)公式について。数学B:数列の和
数列 【2021千葉大学】外接する３つの円と直線、等比数列・等比中項(a,b,cがこの順で等比数列)
２円の位置関係(外接する)と等比数列・等比中項の融合問題。２円が外接し、直線に接することから関係式を作り、a,b,cがこの順で等比数列になることを利用して公比rを求める。2021千葉大学過去問演習。数学A：図形と計量、数学B：数列
数列 【2021北海道大学】和と一般項(Snとan)，部分分数分解｜数学B：数列
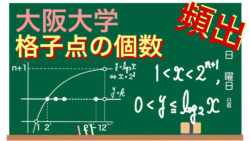n≧2とn=1と場合分けして、和から一般項を求める。分母の積の形から差分数分解し、シグマ(和)をとる部分分数分解の典型問題。分母が２つ残るタイプ。2021北大過去問演習。数学B数列
複素数と方程式 【2021近畿大学・文系】1の立方根の虚数解：ω(オメガ)とは？ωの性質と演習問題
1の3乗根「x^3=1」の虚数解の1つをω。このとき関係式「ω^3=1」「ω^2+ω+1=0」が成り立つ。1,ω,ω^2の周期性、次数下げを用いて考える。数学Ⅱ：複素数と方程式。頻出・有名入試問題。近大過去問。産近甲龍。関関同立。私立大学受験対策。
東京大学 【2015東京大学】曲線の通過領域｜パラメータ(媒介変数)aの存在条件・２次方程式の実数解の存在条件
入試頻出の通過領域(逆手流・逆像法)の考え方。aの方程式と考え、正の範囲に少なくとも1つの実数解をもつ(解の配置：2次関数)を考える．2015東大過去問演習・対策。２次試験。数学Ⅱ：図形と方程式。
式と証明 【1995東京大学】√x+√y≦k√(2x+y)のkの最小値｜コーシー・シュワルツの不等式
受験数学における有名・頻出不等式(相加平均・相乗平均の関係、コーシー・シュワルツの不等式、三角不等式)の問題の１つであるコーシー・シュワルツの不等式を利用した解法。1995東大過去問演習・対策。２次試験。数学Ⅱ：不等式の証明・最大・最小値
東京大学 【2003東京大学】円周率が3.05より大きいことを証明せよ｜円周率とは？
円周率πとは円の直径に対する円周の長さの比。円に内接する正十二角形の周の長さの総和と円周の長さの大きさの大小から証明する。一行問題。有名。2003東大過去問演習。
ベクトル 【2008京都大学】平行四辺形の頂点となるものが存在する証明｜１次独立なベクトルの利用
ベクトルにおける最重要・基本事項の「一次独立」について、差がつく良問。一次独立なベクトルの線形和を用いて、平行四辺形の存在証明。2008京都大学・乙[第３問]過去問演習、過去問対策。数学B空間ベクトル
京都大学 【2019京都大学】半径1の球面上の5点の四角錐の体積の最大｜微分
底面を固定し、高さを最大にする四角錐の体積の最大を求める典型・頻出問題。体積を３次関数で表し、微分、増減表を利用して考える。2019京大過去問演習。数学Ⅱ微分積分の最大最小。
共通テスト(センター試験) 【2018センター試験】数学ⅡB：第４問平面ベクトル｜三角形の内分点、一次独立、内積
三角形の内分点と内積の典型的な基礎基本の計算問題。一次独立。大学共通テスト対策。センター試験過去問演習。数学ⅡBベクトル
共通テスト(センター試験) 【2019センター試験】数学ⅡB：第４問ベクトル｜四角錐・等脚台形・垂線の長さ
四角錐・三角錐に関する空間ベクトル。底面が等脚台形。体積の高さを求める典型問題。大学共通テスト対策。センター試験過去問演習。数学ⅡBベクトル
共通テスト(センター試験) 【2020センター試験】数学ⅡB：第４問ベクトル｜内積の計算と四面体の体積
空間ベクトルの成分、内積の計算。同一平面にある条件(共面条件)の利用、四面体の体積をもとめる基礎基本・標準レベルの問題。大学共通テスト対策。センター試験過去問演習。数学ⅡBベクトル
京都大学 【2019京都大学・理系】cosθは無理数,cos2θとcos3θがともに有理数となるθ
数学Ⅱの三角関数と有理数・無理数の論証問題の融合問題。２倍角、３倍角の公式、背理法を利用。標準的良問。2019京大過去問・対策・演習。
2021年入試問題 【2021広島大学】y=cos3x,y=cos7x(x≧0)の共有点について｜数学Ⅱ：三角関数
sin5xをsinxで表す。cosA=cosBの解について。cos(12/5)πの値を求める。三角関数：加法定理、２倍角、３倍角、半角の公式の利用。広島大学過去問演習。差がつく頻出問題。