 場合の数・確率
場合の数・確率 【2021共通テスト(第1日程)】数学ⅠA:第3問(場合の数と確率)|条件付き確率,会話形式
複数の箱からくじを引く試行についての条件付き確率。太郎と花子の会話形式の新傾向の問題。大学共通テスト対策。センター試験過去問演習。数学ⅠA:場合の数と確率
 場合の数・確率
場合の数・確率  共通テスト(センター試験)
共通テスト(センター試験)  共通テスト(センター試験)
共通テスト(センター試験)  場合の数・確率
場合の数・確率  整数問題
整数問題  整数問題
整数問題  2022年入試問題
2022年入試問題  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題 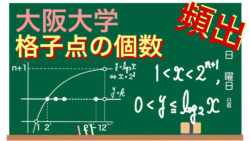 数列
数列  数列
数列  数列
数列  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  図形の性質
図形の性質 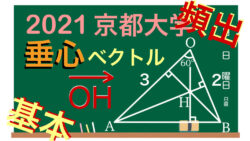 ベクトル
ベクトル 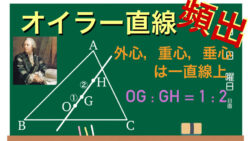 ベクトル
ベクトル  分野まとめ
分野まとめ  分野まとめ
分野まとめ  数列
数列  整数問題
整数問題  整数問題
整数問題