 2021年入試問題
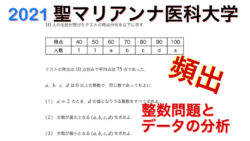
2021年入試問題 【2021聖マリアンナ医科大学】データの分析と整数問題|分散の最大・最小
データの分析と整数問題の融合。データの分析(平均値、中央値(メジアン)、最頻値(モード)、分散、標準偏差、共分散、相関係数)の公式確認。入試問題演習。共通テスト対策、2次試験対策数学演習。医学部。
 2021年入試問題
2021年入試問題  整数問題
整数問題  式と証明
式と証明  三角関数
三角関数  整数問題
整数問題  場合の数・確率
場合の数・確率  複素数と方程式
複素数と方程式  2021年入試問題
2021年入試問題  整数問題
整数問題  場合の数・確率
場合の数・確率  整数問題
整数問題  共通テスト(センター試験)
共通テスト(センター試験)  整数問題
整数問題  整数問題
整数問題  場合の数・確率
場合の数・確率  整数問題
整数問題  整数問題
整数問題  整数問題
整数問題  集合と命題
集合と命題  共通テスト(センター試験)
共通テスト(センター試験)  複素数と方程式
複素数と方程式  式と証明
式と証明 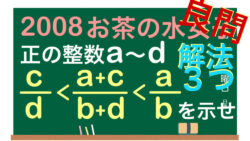 式と証明
式と証明  集合と命題
集合と命題