【数学Ⅱ微分・積分まとめ】絶対におさえておきたい頻出・重要問題まとめ！

以下の問に答えよ．

(１)　京都薬科大学

微分係数 \(f^{\prime} (5)\) の定義に基づいて，

\(\displaystyle\lim_{x\rightarrow 5} \displaystyle\frac{5f(x)-xf(5)}{x-5}\) を \(f(5)\) , \(f^{\prime}(5)\) を用いて表せ．

(２)　防衛大学

関数 \(f(x)\) が \(x=a\) で微分可能なとき，\(\displaystyle\lim_{h\rightarrow 0} \displaystyle\frac{f(a+h)-f(a-2h)}{h}\) を\(f^{\prime} (a)\) を用いて表せ．

【問題１】

曲線 \(y=x^3+x^2+ax\) と放物線 \(y=x^2-2\) は、ともにある点 \(P\) を通り、\(P\) において共通の接線をもつ．このとき、定数 \(a\) の値を求めよ．

【問題２】

2 つの曲線 \(y=x^2\) 、\(y=-x^2+4x-4\) の共通接線の方程式を求めよ．

\(3\) 次関数 \(f(x)=ax^3+bx^2+cx+d\) は \(P\) \(\left(-\displaystyle\frac{b}{3a} , f \left(-\displaystyle\frac{b}{3a}\right)\right)\) に関し点対称なグラフになることを示せ．

\(f(x)=2x^3-9x^2+6x\)

の極大値を \(M\) ，極小値を \(m\) とするとき，以下の値を求めよ．

①　\(M+m\)

②　\(M-m\)

【2020大阪市立大学・文系(一部)】

\(a\) , \(b\) を実数とする．\(3\) 次関数 \(f(x)=x^3+3ax^2+3bx\) に対して，次の問に答えよ．

問１．\(f(x)\) が極大値と極小値をもつための \(a\) , \(b\) の条件を求めよ．

問２．問１の条件が成り立つとする．このとき，\(f(x)\) の極大値の絶対値と極小値の絶対値が等しくなるための \(a\) , \(b\) の条件を求めよ．

【2020東京電機大・理工】

\(3\) 次関数 \(f(x)\) は \(x=-1\) で極大値 \(7\) をとり，\(x=3\) で極小値 \(-25\) をとる．

\(f(x)\) を求めよ．

【2021名城大学】

関数 \(f(x)=x^3-3x^2+4\) を考える．\(xy\) 平面上に曲線 \(C\) : \(y=f(x)\) について，次の問に答えよ．

(１)　\(C\) 上の点 \(P (p,p^3-3p^2+4)\) における接線 \(l\) の方程式を \(p\) を用いて表せ．

(２)　点 \(A(0,a)\) ( ただし，\(a\) は実数 ) を通る \(C\) の接線の本数を求めよ．

【2019早稲田大学・教育】

放物線 \(y=x^2\) 上の点 \((a,a^2)\) における接線と曲線 \(y=x^3-ax\) が異なる \(3\) 点で交わるとき，\(a\) のとりうる値の範囲を求めよ．

【2019京都大学(文理共通)第５問】

半径 \(1\) の球面上の \(5\) 点 \(B_{1}\)，\(B_{2}\)，\(B_{3}\)，\(B_{4}\) は，正方形 \(B_{1}B_{2}B_{3}B_{4}\) を底面とする四角錐をなしている．この \(5\) 点が球面上を動くとき，四角錐 \(AB_{1}B_{2}B_{3}B_{4}\) の体積の最大値を求めよ．

正の実数 \(x , y , z\) において \(x^3+y^3+z^3≧3xyz\) を示せ．

【2021北海道情報大学】

\(\displaystyle\int^{x}_{a}f(t) \enspace dt=4x^3-3x^2+x-\displaystyle\int^{1}_{0}f(t) \enspace dt\)

を満たす関数 \(f(x)\) を考える．ただし \(a\) は実数の定数である．

(１)　関数 \(f(x)\) を求めよ．

(２)　定数 \(a\) の値を求めよ．

【2022大阪大学・文】

以下の問いに答えよ．

(１)　実数 \(\alpha\)，\(\beta\) に対し

\(\displaystyle\int^{\beta}_{\alpha}(x-\alpha)(x-\beta)dx=\displaystyle\frac{(\alpha-\beta)^3}{6}\)

が成り立つことを示せ．

(２)　\(a\)，\(b\) を \(b>a^2\) を満たす定数とし，座標平面上に点 \(A\) \((a,b)\) をとる．さらに，点 \(A\) を通り，傾きが \(k\) の直線を \(l\) とし，直線 \(l\) と放物線 \(y=x^2\) で囲まれた部分の面積を \(S(k)\) とする．\(k\) が実数全体を動くとき，\(S(k)\) の最小値を求めよ．

【2022京都大学・文】

\(xy\) 平面上の \(2\) 直線 \(L_{1}\) , \(L_{2}\) は直交し，交点の \(x\) 座標は \(\displaystyle\frac{3}{2}\) である．また，\(L_{1}\) , \(L_{2}\) はともに曲線 \(C\) : \(y=\displaystyle\frac{x^2}{4}\) に接している．

このとき， \(L_{1}\) , \(L_{2}\) および \(C\) で囲まれる図形の面積を求めよ．

曲線 \(y=x^3-4x\) と，その曲線上の点 \(( 1 , -3 )\) における接線で囲まれた図形の面積 \(S\) を求めよ．

【2022慶應義塾大学】

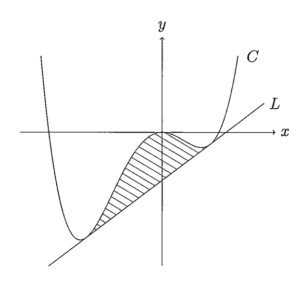
\(xy\) 平面上の曲線 \(C\) を \(y=x^2(x-1)(x+2)\) とする．

(１)　\(C\) に \(2\) 点で下から接する直線 \(L\) の方程式を求めよ．

(２)　\(C\) と \(L\) が囲む図の斜線部分の面積を求めよ．

【2021大阪府立大学】

\(a\) を正の実数とする．関数 \(S(a)=\displaystyle\int^{2}_{0}| x^2-ax |\enspace dx\) について，以下の問に答えよ．

(１)　\(x\) の関数 \(y=| x^2-ax |\) のグラフの概形をかけ．

(２)　\(S(a)\) を \(a\) を用いて表せ．

(３)　 \(a\) がすべての正の実数を動くとき，\(S(a)\) の最小値を求めよ．

【2018一橋大学】

\(a\) を実数とし，\(f(x)=x-x^3\) , \(g(x)=a(x-x^2)\) とする．\(2\) つの曲線 \(y=f(x)\) , \(y=g(x)\) は \(0<x<1\) の範囲に共有点を持つ．

(１)　\(a\) のとりうる値の範囲を求めよ．

(２)　\(y=f(x)\) と \(y=g(x)\) で囲まれた \(2\) つの部分の面積が等しくなるような \(a\) の値を求めよ．

曲線 \(C\)：\(y=x^3-4x\) 上の点 \(1,-3\) における接線 \(L\)：\(y=-x-2\) となる．

このとき，曲線 \(C\) と接線 \(L\) の交点を求めよ．